|
|

C’est ce que vous permet de réaliser le modèle Black-Scholes en calculant la valeur théorique de cette option. Ce modèle est une équation mathématique qui vous permet de déterminer le prix qu’une option devrait avoir. Si le prix proposé par le marché ne coïncide pas avec cette valeur calculée, vous pouvez, au titre de la théorie de l’efficience et de la rationalité des marchés, anticiper une évolution du prix de l’option vers sa valeur théorique.
Lisez notre article pour tout savoir sur cette formule magique. Si vous cherchez un courtier pour investir dans les options, cliquez ici.
Modèle Black-Scholes
Qu’est-ce que le modèle Black-Scholes ?
Le modèle Black-Scholes est un outil qui permet de calculer la valeur théorique d’une option. Cette formule mathématique a été élaborée par Fischer Black et Myron Scholes, deux professeurs de finance de l’université de Chicago. Les deux universitaires ont commencé à travailler sur cette formule dans les années 1960, en s’inspirant des travaux de Paul Samuelson, qui avait publié en 1965 une formule destinée à évaluer le prix d’une option. Black et Scholes ont amélioré la formule de Samuelson en tenant compte de la volatilité du prix de l’actif sous-jacent. En 1997, Black, Scholes et Merton ont reçu le prix Nobel d’économie pour leur travail sur la formule à laquelle ils ont donné leur nom.
Fischer Black est né en 1938 à Washington, D.C. Il a obtenu un doctorat en économie de l’Université de Chicago en 1964. Après avoir travaillé comme chercheur à la Banque de réserve fédérale de New York, il a rejoint la faculté de l’Université de Chicago en 1969. Il est décédé en 1995 à New York. Myron Scholes est né en 1941 à Toronto, au Canada. Il a obtenu un doctorat en économie de l’Université de Chicago en 1970. Après avoir travaillé comme chercheur au Massachusetts Institute of Technology, il a intégré la faculté de l’Université de Stanford en 1974.
Le modèle Black-Scholes aujourd’hui
La formule Black-Scholes a été publiée pour la première fois en 1973 par Fischer Black, Myron Scholes et Robert Merton dans un article intitulé “The Pricing of Options and Corporate Liabilities”. Depuis, elle résiste à l’épreuve du temps. Elle est aujourd’hui largement utilisée dans le monde de la finance. Avec le passage de la négociation sur le parquet à la négociation électronique, tous les prix sont maintenant calculés par des ordinateurs avant d’être affichés à l’écran. Il y a quelques décennies, les cours étaient encore calculés manuellement par les teneurs de marché. Mais, de nos jours, ce sont les ordinateurs qui ont repris le flambeau. Vous n’avez bien évidemment pas besoin de connaître cette formule. Car les cours acheteur et vendeur des options sont calculés automatiquement par des ordinateurs sur la base de celle-ci (ou une variante de celle-ci).
Quels sont les paramètres du modèle Black-Scholes ?
Dans l’image ci-dessous, nous présentons la formule qui constitue le modèle Black-Scholes :
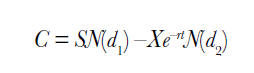
C = valeur théorique d’un call de style européen
S = prix d’une action qui ne rapporte pas de dividendes
X = prix d’exercice
t = temps qu’il reste avant l’échéance (exprimé en années)
σ = écart type annuel (volatilité) du prix de l’action (exprimé sous forme de pourcentage)
r = taux d’intérêt annuel
ln = logarithme naturel
e = fonction exponentielle
N = fonction de distribution cumulative normale
On voit que, pour calculer la valeur théorique d’une option à l’aide du modèle Black-Scholes, il faut connaître cinq propriétés appartenant à cette option ou à son sous-jacent :
- Le prix d’exercice de l’option
- Le temps qu’il reste avant l’échéance de l’option
- Le prix actuel du sous-jacent
- Le taux d’intérêt qui s’applique pendant la vie de l’option
- La volatilité du sous-jacent
Passons en revue ces paramètres clés.
Le prix d’exercice
Le prix d’exercice d’une option (strike price en anglais) est le prix auquel l’acheteur de l’option a le droit d’acheter (dans le cas des options d’achat) ou de vendre (dans le cas des options de vente) le sous-jacent. Ce prix ne peut varier car il fait partie des termes qui constituent le contrat d’option. Une option d’achat dont le prix d’exercice est 50 ne peut pas changer de prix d’exercice au cours de la vie de l’option et adopter, par exemple, le strike 40.
Temps qu’il reste avant l’échéance
Pour déterminer la valeur d’une option, il faut connaître le temps qui sépare cette option de son échéance. Car cela permet, entre autres choses, de calculer les chances de voir l’option expirer dans la monnaie.
Lorsqu’on renseigne dans le modèle Black-Scholes le temps qu’il reste à une option avant d’arriver à échéance, il convient de renseigner un nombre annualisé. Si, par exemple, le temps restant avant l’échéance s’élève à 73 jours, il convient d’entrer le nombre suivant : 73 / 365 = 0,2.
Le prix du sous-jacent
La valeur d’une option dépend de la probabilité qu’elle a d’expirer dans la monnaie dépend. Or, cette probabilité dépend de la distance qui sépare le prix d’exercice de l’option du prix actuel du sous-jacent. Il convient donc de renseigner cette dernière valeur lorsqu’on veut calculer la valeur théorique d’une option à l’aide d’un modèle tel que celui de Black et Scholes.
Les taux d’intérêt
Parmi toutes les valeurs qui composent le modèle Black-Scholes, les taux d’intérêt représentent sans doute la valeur qui joue le rôle le moins important. Seules les positions très importantes, qui comprennent de nombreux contrats, peuvent être significativement impactées par une évolution des taux d’intérêt.
Les taux d’intérêt ont une double importance dans l’évaluation d’une option. Tout d’abord, ils peuvent avoir un impact sur le prix à terme (forward price) du sous-jacent. Une hausse des taux d’intérêt peut faire augmenter ce prix à terme et faire ainsi augmenter la valeur des calls mais diminuer celle des puts. De plus, les taux d’intérêt peuvent avoir un imapct sur le coût de portage (present value) d’une option.
Mais quel est le taux qu’il convient de renseigner pour évaluer une option à l’aide du modèle Black-Scholes ? Les traders peuvent se tourner vers le taux d’intérêt dit « sans risque », c’est-à-dire le taux offert par un emprunteur d’excellente qualité.
La volatilité
Comme nous l’avons vu, la volatilité dont tient compte le modèle Black-Scholes pour calculer la valeur d’une option est l’écart type annuel du sous-jacent (exprimé sous la forme d’un pourcentage). La volatilité est une mesure de la distribution des prix d’un actif sur une période donnée. Elle est exprimée en pourcentage et est calculée à l’aide de l’écart type. L’écart type est une mesure statistique qui indique la distance moyenne entre les valeurs d’une série et la moyenne de cette série. Plus l’écart type est élevé, plus les valeurs sont dispersées autour de la moyenne et plus la volatilité est élevée.
Comment tirer profit du modèle Black-Scholes ?
Il existe d’autres modèles pour évaluer les options. Le modèle binomial, par exemple, propose une méthode numérique pour l’évaluation des options. Mais le modèle Black-Scholes reste le plus renommé.
Il peut y avoir un écart entre le prix réel d’une option, autrement dit l’évaluation faite par le marché, et la valeur que nous pouvons attribuer à cette option à l’aide du modèle Black-Scholes. Dans ce type de scénario, un trader peut avoir intérêt à vendre les options que le marché surévalue et à acheter les options que le marché sous-évalue.
Investir dans les options via LYNX
Dans la plateforme de trading professionnelle TWS, vous disposez de nombreux outils pour trader vos options de manière professionnelle. Vous pouvez notamment afficher, dans votre chaîne d’options, la valeur des grecques des options qui vous intéressent, lesquelles grecques sont calculées à partir du modèle Black-Scholes. Découvrez comment trader les options via LYNX :
Sources
Sheldon Natenberg, Option Volatility and Pricing Advanced Trading Strategies and Techniques, Mc Graw Hill Education, second edition


